19. óra - Függvények alkalmazása

A másodfokú egyenlet megoldása (TK. 9.)

Az ax^2+bx+c=0
egyenlet gyökei: x_{1,2} = {-b \pm \sqrt{b^2-4ac} \over 2a}.

from math import sqrt
def mfegy(a,b,c):
    return (-b+sqrt(b**2-4*a*c))/2*a,(-b-sqrt(b**2-4*a*c))/2*a
print(mfegy(1,-2,-3))

20. óra - Egyenletmegoldás ciklussal

Newton iteráció TK. 117. (1.e. megoldás) x_{n+1}=x_n-\frac{f\left(x_n\right)}{f'\left(x_n\right)},n=[0,1,...]

fx = lambda x: 2*x**3 - 3*x + 1
Df = lambda x: 6*x**2 - 3
xn = 0
for n in range(0,10):
    print(xn) # Megoldásközelítés az n. iterációban.
    xn = xn - fx(xn)/Df(xn)

21. óra - Függvények alkalmazása (rekurzió)

Hanoi tornyai (TK. 61.)

n=1 -re h(n,a,b) = a \longrightarrow b egyébként (minden n>1 egész számra):
h(n,a,b) = h(n-1,a,6-a-b), a \longrightarrow b, h(n-1,6-a-b,b)

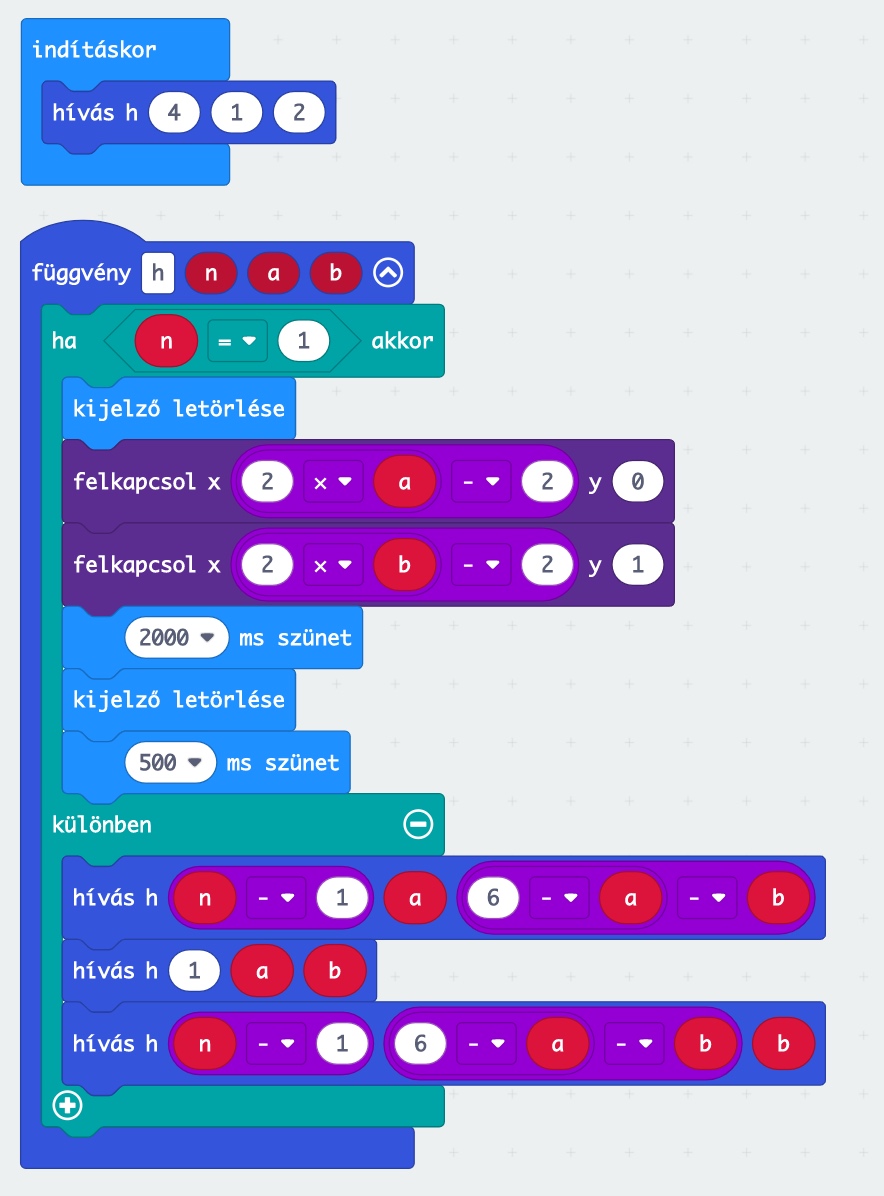
def h(n, a, b):
    if ( n == 1 ):
        return "( {} => {} )".format(a, b)
    else:
        return (
            h( n-1, a,     6-a-b )+
            h( 1,   a,     b )+
            h( n-1, 6-a-b, b )
        )
print( h( 3, 1, 2 ) )

micro:bit blocks

letöltés

22. óra - Teknőcgrafika + rekurzív fügvény

from turtle import *
speed("fastest")
color("red","blue")
def k(x):
    for i in range(6):
        forward(x)
        left(60)
    left(10)
    if x>8:
        k(34*x/35)
begin_fill()
k(250)
end_fill()
mainloop()

Python kiegészítő anyagok a 10. évfolyam számára